Background Knowledge

Relevant lectures: 3.1T, 3.1F

This chapter contains some math about the mean, variance, and guassian functions, image processing topics such as SIFT, and a summary of similarity and distance measures relevant to this course.

Math

Mean and Variance of a Discrete Random Variable

The mean μ (mu) of a discrete random variable X is the weighted sum over the possible outcomes of X:

• μ = E(X) = sum([p(X_i) * X_i for i in range(N)])

The variance σ^2 (sigma squared) of a random variable is:

• σ^2 = E(X - E(X))^2

Gaussians

A guassian function is characterized by its μ (mean) and σ^2 (variance).

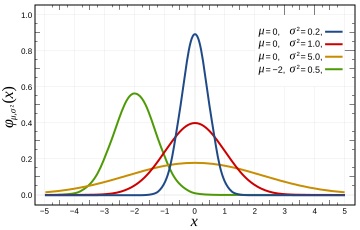
(Extra reading: Stanford Coursera course; Image source: wikipedia)

Bayes’ Rule

Bayes’ rule describes the probability of an event, based on prior knowledge of conditions that might be related to the event. For example, if cancer is related to age, then, using Bayes’ theorem, a person’s age can be used to more accurately assess the probability that they have cancer, compared to the assessment of the probability of cancer made without knowledge of the person’s age (Wikipedia).

Mathematically, it is expressed as P(A|B) = (P(B|A) * P(A)) / (P(B)), which is read as “the probability of A given B is the probability of B given A times the probability of A divided by the probability of B.”

Image Processing

SIFT

“Scale-invariant feature transform (SIFT) is an algorithm in computer vision to detect and describe local features in images” (Wikipedia). Its exact workings are not too important for this course; it is mainly key to know that it acts as both detector and descriptor.

Similarity and Distance Measures

Similarity and distance measures are used to quantify how alike two things (represented as vectors) are.

Boolean Match

Boolean matching is a measure of the similarity between strings.

• It is defined as “the count of the symbol types common to two strings” (slides).
• Symbol tokens are instances of words, or “running words” (slides).
  • The phrase “a dog chases a cat” has the following word tokens: ['a', 'dog', 'chases', 'a', 'cat'].
• Symbol types are dictionary of distinct words (slides)
  • The phrase “a dog chases a cat” has the following word tokens: ['a', 'dog', 'chases', 'cat']. Note that 'a' only occurs once.

Example: The boolean match between “a dog chases a cat” and “a cat chases a mouse” is 3 (common symbol types are ['a', 'chases', 'cat']).

Jaccard Similarity Coefficient

The Jaccard similarity coefficient (also known as Jaccard index and Intersection over Union) is a measure of the similarity between sets.

• It is defined as the size of the intersection (elements in both sets) divided by the size of the union (elements in either set).

Example: The Jaccard similarity coefficient between {Harry, Ron, Hermione} and {Harry, James, Lily} is 0.2 (intersection is {Harry} and union is {Harry, Ron, Hermione, James, Lily}).

(Source + extra reading: Wikipedia)

Manhattan Distance

Manhattan distance (also known as L_1 distance, Taxicab distance, cityblock distance, and Manhattan length) is a measure of the distance between two points in Euclidean plane.

• It is defined as “the sum of the lengths of the projections of the line segment between the points onto the coordinate axes” (Wikipedia).
• In two dimensions, it is simply the count of steps “up” (or “down”) the grid plus the count of steps “left” (or “right”) the grid, to get from point A to point B.

Example: The Manhattan distance between point A at (1,0) and point B at (5,3) is 7 (“right” 4 from 1 to 5, and “up” 3 from 0 to 3).

(Source + extra reading: Wikipedia)

Euclidean Distance

The Euclidian distance (also known as L_2 distance) is a measure of the distance between two points in Euclidean plane.

• It is defined as the length of the line segment connecting the points A and B
• It can be calculated using the Pythagorean formula (sqrt((A.x - B.x)^2 + (A.y - B.y)^2))
• It generalizes to n dimensions

Example: The Euclidian distance between point A at (1,0) and point B at (5,3) is 5.

(Source + extra reading: Wikipedia)

Euclidean Distance Between Normalized Vectors

The Euclidian distance between normalized vectors is a measure of the distance between two vectors.

• It is defined as the Euclidian distance between normalized versions of vectors A and B.

Example: The Euclidian distance between normalized vectors of point A at (1,0) and point B at (5,3) is ~0.7 (A normalized is (1,0) and B normalized is (5/sqrt(34), 3/(sqrt(34))).

Dot Product

The dot product (also known as the scalar product and inner product) is a measure of the similarity between two vectors.

• It is defined as the sum of the multiplication of each element in vectors p and q.
• As a Python expression: sum([p[i] * q[i] for i in range(len(p))]).

Example: the dot product of vectors [1, 3, -5] and [4, -2, -1] is 3 (1*4 + 3*-2 + -5*-1 = 3).

(Source + extra reading: Wikipedia)

Cosine Similarity

Cosine similariy is a measure of the similarity between two vectors.

• It is defined as the cosine of the angle between two vectors.
• It can be calculated by dividing the dot product of the two vectors by the multiplication of their magnitudes.
• “Two vectors with the same orientation have a cosine similarity of 1, two vectors at 90° have a similarity of 0, and two vectors diametrically opposed have a similarity of -1, independent of their magnitude” (Wikipedia).

Example: The cosine similarity of [5, 0, 3, 0, 2, 0, 0, 2, 0, 0] and [3, 0, 2, 0, 1, 1, 0, 1, 0, 1] is 0.94 (SlideWiki).

(Source + extra reading: Wikipedia)

Adjusted Cosine Similarity

Adjusted cosine similarity is common for recommender systems.

• It is defined as the cosine similarity on mean-centered vectors.
  • A Mean-centered vector is the vector minus the average of all its elements

Example: The adjusted cosine similarity of [1, 2, 3] and [3, 4, 5] is 0 ([1, 2, 3] - 2 = [-1, 0, 1] and [3, 4, 5] - 4 = [-1, 0, 1], so the mean-centered vectors are the same).

Pearson correlation

Pearson correlation is a measure of the linear correlation between two vectors that is common for recommender systems.

• It is defined as “the covariance of the two variables divided by the product of their standard deviations” (Wikipedia).
• It is invariant to how the user uses the rating system.

(Source + extra reading: (Wikipedia)

Spearman rank correlation

Spearman rank correlation (also known as Spearman’s rho) is a measure of the similarity of two ranked lists.

• It is defined as “the Pearson correlation coefficient between the ranked variables” (Wikipedia).
• If the ranks are integers, it can be calculated using: 1 - sum([pow(x,2) for x in d]) / (n * (pow(n,2)-1))), where d[i] is the difference between the two ranks of each observation.

Example: Wikipedia has a good example.

(Source + extra reading: (Wikipedia)

[ Home ]